Evolute of the Euler spiral

The evolute of the Euler spiral has a simple representation as a Cesàro equation. Evolutes of curves are interesting because the Nehab 2020 paper shows us that for strongly correct stroke expansion, the evolute of a curve is needed in addition to the parallel curve (see Figure 11 and related discussion). This page contains that derivation, as well as related results on near-optimal flattening of the evolute to line segments.

In this image, the Euler spiral segment is in gray, and its evolute is in blue:

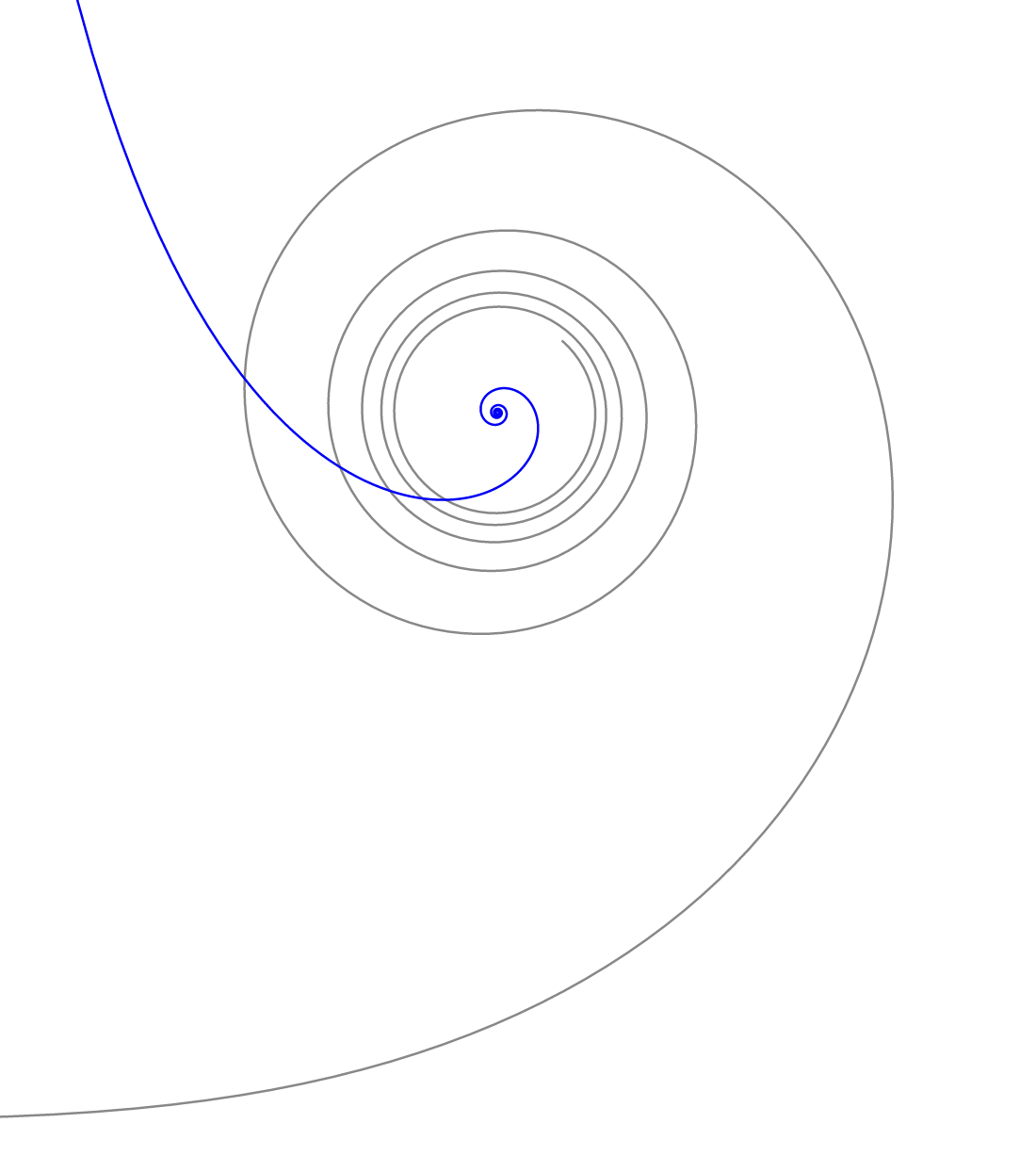
Image of Euler spiral and its evolute

We'll start with an Euler spiral defined (in Cesàro form) as follows:

$$\kappa(s) = as$$

Integrating this equation results in the Whewell form:

$$\theta(s) = \frac{as^2}{2}$$

And we have an equation for the derivative of the curve. In this derivation, we'll fluidly mix complex numbers and 2D vectors, writing unit vector in the direction of $\theta$ as $e^{i\theta}$. This choice, while a bit of an abuse of notation, will be very convenient when calculating derivatives.

$$x'(s) = e^{i\theta(s)} = e^{i\frac{as^2}{2}}$$

$$x''(s) = iase^{i\frac{as^2}{2}} = iasx'(s)$$

The evolute is defined as points offset from the source curve in the normal direction, by the radius of curvature. Generally:

$$\bar{x}(s) = x(s) + \frac{ie^{i\theta(s)}}{\kappa(s)}$$

Plugging in the Euler spiral, we can thus easily obtain the derivative of the evolute with respect to the s parameter.

$$ \begin{align} \bar{x}'(s) &= x'(s) + \frac{i^2asx'(s)}{as} - i\frac{x'(s)}{as^2} \\ &= -i\frac{x'(s)}{as^2} \end{align} $$

Proceeding, we'll get the arc length (using s, arc length along original Euler spiral, as a parameter), and also obtain a second derivative for use in calculating the curvature.

$$\bar{s}'(s) = |x'(s)| = \frac{1}{as^2}$$

$$\bar{s}(s) = -\frac{1}{as}$$

A note: the formula for arc length follows readily from a well-known result in differential geometry, as cited in the Stoer paper (the bottom of page 322). However, given that we already have the derivatives for the purpose of computing curvature, it's maybe easier to just derive than rely on a cited method.

$$\bar{x}''(s) = \frac{x'(s)}{s} + 2i\frac{x'(s)}{as^3}$$

When computing the cross-product for the standard curvature formula, the second term above drops out because it's in the same direction as the first derivative, while the first is orthogonal.

$$ \begin{align} \bar{\kappa}(s) &= \frac{\bar{x}'' \times \bar{x}'}{|\bar{x}'|^3} \\ &= \frac{1}{as^3} / \frac{1}{a^3 s^6} \\ &= a^2 s^3 \end{align} $$

And then this gives the Cesàro equation for the evolute in terms of its own arc length:

$$\bar{\kappa}(\bar{s}) = -\frac{1}{a\bar{s}^3}$$

General evolute of log-aesthetic curves

The family of curves in which curvature is a power of the arc length is called "log-aesthetic curves," and there is a small industry of papers on this curve family. This family is closed under evolute, see Yoshida & Saito 2012 for the result.

Thus, the formula derived in this page is an instance of the general result, and is also shown in Figure 3(c) of the above cite. In general, the evolute of the curve defined by $\kappa(s) = s^\gamma$ is another curve with $\kappa(s) = s^{-\frac{1 + 2\gamma}{\gamma}}$. (There may be a uniform scaling factor; someone should go over the math in detail)

Subdivision density

Following the derivation for the parallel curve of the Euler spiral, the subdivision density for flattening to lines of a curve with respect to the source curve parameter s is given by this formula:

$$\rho(s) = \sqrt{0.125|\bar{\kappa}(s)|}\frac{d\bar{s}}{ds}$$

Plugging in the formulae above and simplifying, we get:

$$\rho(s) = \sqrt{\frac{1}{8s}}$$

And to do subdivision, we need the integral of this (and its inverse):

$$\int_0^t\rho(s)dt= \sqrt{\frac{t}{2}}$$

Thus, finding the subdivision points for near-optimal flattening of an Euler spiral evolute is even simpler than the flattening of the Euler spiral itself, much less the parallel curve of an Euler spiral.

References